Вторая проблема, касающаяся того, что приходится иметь дело с таким количеством родительских переменных, которое в принципе может стать бесконечным, решается благодаря принятию так называемого марковского предположения, или предположения о марковости, которое заключается в том, что текущее состояние зависит лишь от конечной истории предыдущих состояний. Процессы, соответствующие этому предположению, были впервые глубоко исследованы российским ученым-статистиком Андреем Марковым и называются марковскими процессами, или марковскими цепями. Существует несколько разновидностей таких процессов; простейшим из них является марковский процесс первого порядка, в котором текущее состояние зависит только от предыдущего состояния и не зависит от каких-либо более ранних состояний. Иными словами, состояние — это информация, которая требуется для того, чтобы сделать прогноз о будущем независимым от прошлого, если дано это состояние. С использованием принятой в этой главе системы обозначений соответствующее утверждение об условной независимости позволяет сформулировать для всех t следующее соотношение:

(15.1)

Таким образом, в марковском процессе первого порядка законы, описывающие, как состояние развивается во времени, полностью представлены в условном распределении, которое мы будем называть моделью перехода для процессов первого порядка2. Моделью перехода для марковского процесса второго порядка является условное распределение. Структуры байесовских сетей, соответствующие марковским процессам первого и второго порядка, приведены на рис. 15.1.

Рис. 15.1. Структуры байесовских сетей: байесовская сеть, соответствующая марковскому процессу первого порядка с состоянием, определяемым переменными Xt (а); марковский процесс второго порядка (б)

Кроме ограничения количества родительских переменных, относящихся к переменным состояния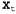, необходимо ограничить количество родительских переменных, относящихся к переменным свидетельства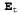. Как правило, в данной главе предполагается, что переменные свидетельства во время t зависят только от текущего состояния:

(15.2)